Number theory and Group theory

In this section and other sections of this page we will analyze an open problem in number theory regarding binomial coefficients. We examine the following condition: Condition 1. For a positive integer n, there exist prime p and r such that if 1 £ k £ n-1 then the binomial coefficient C(n,k) is divisible by at least one of p or r. Then a very natural question follows: does Condition 1 hold for all integers n?

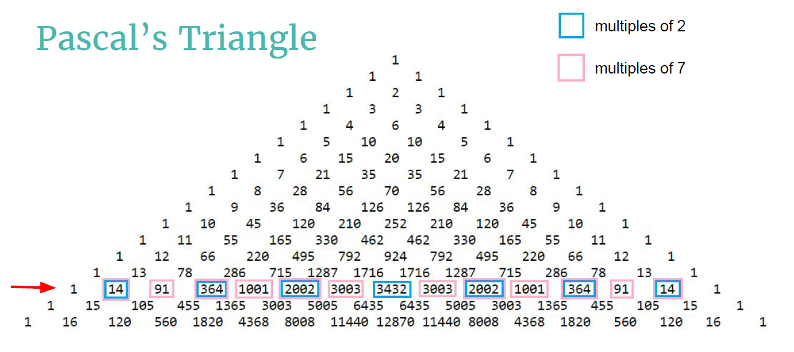
We can visualize Condition 1 using Pascal¢s Triangle. We fix some n and then we look at the n^th row of Pascal¢s Triangle. We want to see if it is true that we can find two primes p and r such that if we paint the multiples of p in the n^th row with one color and the multiples of r in the n^th row with another color, then all the numbers in the n^th row are painted either with one of the colors, the other, or both (ommiting the ones in the edges). The following picture illustrates this explanation with n=14, p=2 (blue) and r=7 (pink).

In this page we will talk about some cases in which we can prove that n satisfies Condition 1. In the section "Fixing one prime" we provide code and information for when we fix p or r to be a certain prime. In the section "All possible pairs" we evalute given n how many pairs of primes make n satisfy Condition 1. In the section "Multinomials" we study the generalization of Condition 1 for the multinomials. Finally, in the section "OEIS sequences" we give code and explanations for proofs in which certain n satisfy Condition 1, in which we find two sequences that the On-line Encyclopedia of Integer Sequences has published.

First of all, Lucas¢ Theorem is a very useful theorem regarding the divisibility of binomial coefficients. It states the following: Theorem. (Lucas) Let m and n be positive integers and let m = m_kp^k + m_k-1p^k-1 + ... + m₁p + m₀ and n=n_kp^k + n_k-1p^k-1 + ... + n₁p + n₀ be the base p expansions of m and n respectively. Then, C(m,n) º Õ_i=0^k C(m_i,n_i) mod p. It is important to notice that by convention C(m,n) = 0 if m < n. Now we can prove the following statement: Proposition. A positive integer n satisfies the 1-variation of Condition 1 with p if n=p^a for some a>0. Proof: The base p representation of n is equal to 10¼0 with a zeroes. Any k such that 1 £ k £ n-1 has at most a -1 zeroes in base p. Therefore, at least one of the digits of the base p representation of k is bigger than the corresponding digit of n in base p. It then follows from Lucas¢ Theorem that C(n,k) is divisible by p. Otherwise if n is not a prime power and hence some digit of n in base p is not zero we can find at least one k such that C(n,k) is not divisible by p.

From the previous proposition we can derive the following corollary: Corollary. If n=p^a + 1, then p and any prime factor of n satisfy Condition 1. Proof: The proof relies on the fact that C(n,k)+(n,k+1) = C(n+1,k+1) for all positive integers n and k. If n is a power of a prime p, then it follows from the last proposition that C(n+1,k) is divisible by p if 2 £ k £ n-1. When k=1 or k=n, we have that C(n+1,k) = n+1, so any prime factor of n+1 divides it.

We can also prove the following proposition: Proposition. If a positive integer n is equal to the product of two prime powers p₁^a and p₂^b , then n satisfies Condition 1 with p₁ and p₂. Proof: Observe that lcm(p₁^a ,p₂^b ) = n. The base p₁ representation of n ends in a zeroes and the base p₂ representation of n ends in b zeroes. Because any positive k smaller than n cannot be divisible by both p₁^a and p₂^b , we can apply Lucas¢ Theorem modulo the prime p₁ if p₁^a does not divide k or modulo the prime p₂ if p₂^b does not divide k.