Number theory and Group theory

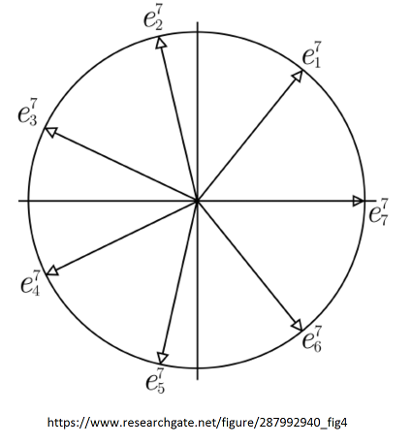
In section "Angles in circle" we could see that somehow we can relate primitive roots and generators to roots of unity by also representing them in the unit circle. Roots of unity are any complex number that if we raise it to a positive integer n it is equal to 1. So roots of unity are any a that satisfies z^a = 1. The following picture illustrates the 7^th roots of unity:

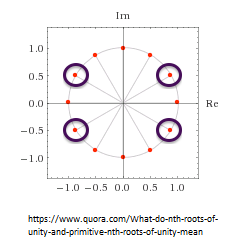
You can observe that they are distributed forming a regular heptagon, and therefore the angle of every root of unity is a multiple of 2 p / 7. This is explained with Euler¢s formula e^ix = cos(x) + isin(x). We can also define the primitive roots of unity, which are any a such that z^a = 1 and is not a k^th root of unity for any k < n. However, note that the primitive roots of unity are the generators! Which means that they are the numbers coprime to n. For example, the following picture illustrates the primitive roots of 12 (the ones that are circled). Among the 12^th roots of unity, only 4 are primitive, because f(12)=4. As you can see in the circle, they are 1, 5, 7 and 11, which are the numbers smaller than 12 that are coprime to 12.

Then a question arises: if for each integer n there is a polynomial, namely xⁿ -1, whose roots are the roots of unity of n, is it possible to find a polynomial whose roots are the generators of n? The answer is yes and they are called cyclotomic polynomials. Hence, the roots of the nth cyclotomic polynomial are the numbers coprime to n. The cyclotomic polynomials are found recursively by applying the following property and using the fact that F₁(x) = x-1: Õ_d|n F_d(x) = xⁿ - 1. This way we can find the first cyclotomic polynomials: F_2(x) = x² -1/ F_1(x) = x² -1 / x-1 = x+1 F_3(x) = x³ -1/ F_1(x) = x³ -1/x-1 = x² +x+1 F_4(x) = x⁴ -1/ F_1(x) F_2(x) = x⁴ -1/x² -1 = x² +1

Hence, we realize that to compute the nth cyclotomic polynomial we need to find all the divisors of n and the cyclotomic polynomial of each divisor. For this reason it is not fast to compute cyclotomic polynomials. However, we observe that there are three cases in which the nth cyclotomic polynomial can be computed directly without recursion: 1. If n is a prime, then F_p(x) = 1 + x + ·s + x^p-2 + x^p-1 since this is the result of dividing x^p -1 by x-1. 2. If n is of the form 2p, then F_2p(x) = 1 - x + x² - ... + x^p-1 . 3. If n is of the form p^k , then F_p^k (x) = 1 + x +... + x^n-2p + x^n-p . Now we want to analyze if there is any relationship between cyclotomic polynomials and primitive roots. The answer is again yes, and by using the aforementioned property of cyclotomic polynomials we see that if we evaluate the primitive roots of n in F_f(n)(x) modulo n the result will be zero. For instance, we know that 2 is a primitive root of 5. Then, f(5) = 4 and the 4th cyclotomic polynomial is x² + 1. By substituting x by 2 in this polynomial modulo 5 we obtain 0: F_4(2) = 2² + 1 = 5 º 0 mod 5.

Therefore, we conclude that another way of finding the primitive roots of n is by computing F_f(n)(x), evaluate x from 2 to n-1 modulo n and see for which integers this is equal to 0. However, as we have seen, finding a cyclotomic polynomial recursively is quite long, so we conclude that this method is only effective if f(n) is of the form 2p or p^k , because then we can find the cyclotomic polynomial instantly.