The p-adic numbers described in "p-adic numbers" actually form an algebraic field, and it should be differentiated from the p-adic integers, which form a ring. But before we define these structures, we should define the concept of group. A group is a set with an opperation that satisfies the following axioms:
4. Inverse element: for each element a of the group, there exists an element a-1
in the group such that a*a-1
|
= e. For example, the group of integers under the opperation of the addition is a group, because it satisfies these last four axioms. Or for example, Zp, which refers to the integers modulo p, is also a group under the addition.
LaTeX4Web 1.4 OUTPUT
The concept of generator is also interesting. A generator of a group, call it g, is an element of the group such that if we keep applying the operation of the group to the generator we obtain all the elements in the group. For example, 1 is a generator of the group of positive integers under the addition, because by adding 1 to itself we can obtain any positive integer. Now let¢s look at the generators of Zn. Imagine we are in Z6, which means that since we are working modulo 6 we only have the integers 0, 1, 2, 3, 4, 5. 0 is not a generator. 1 is a generator. 2 is not a generator because 2+2 = 4 and 2+2+2 = 6 = 0, so we will never reach 1, 3 or 5. The same thing happens with 3 and 4, but 5 is a generator. Maybe you can see that the generators of Zn are the numbers that are coprime to n (see "Totient function"). An interesting remark is that if n is a prime number, then all the numbers in the group are coprime to n. Also note that you can imagine all the elements of Zp placed in the unit circle. If you put the pencil in one of the elements and add it to itself, you will go to another element (axiom of closure). If this first element that you chose is a generator, you will draw a star going through all the elements. Otherwise you will not. Here you can see an example with Z6:
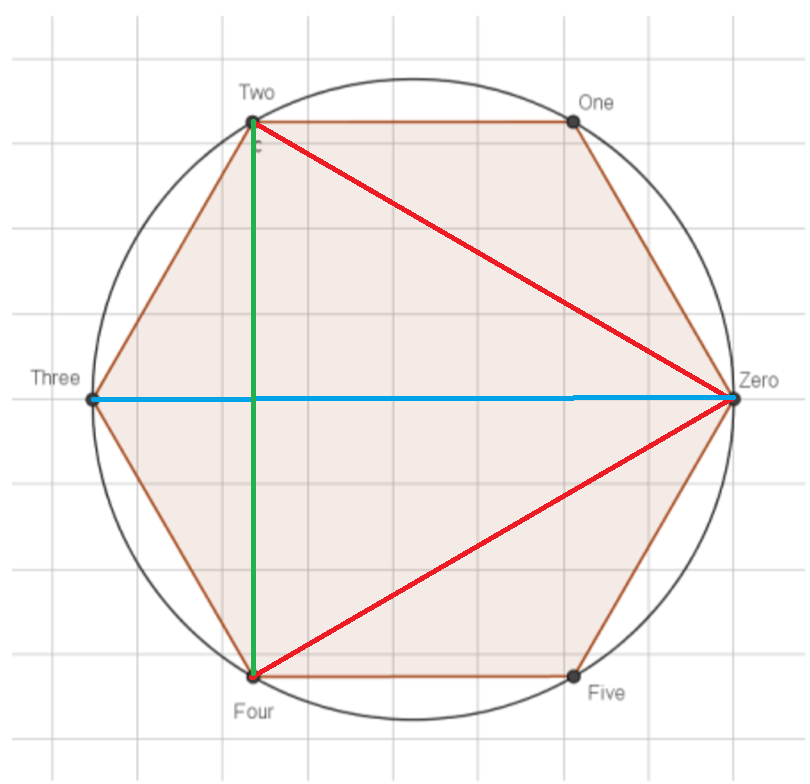
LaTeX4Web 1.4 OUTPUT
Then, p-adic integers form a ring, and why they are not a group is because two operations exist between p-adic integers: addition and multiplication. They are referred to as Zp. Also, p-adic numbers form a field, and why they are not a ring is because they accept inverses. Therefore, we have addition, substraction, multiplication and division. They are referred to as Qp. So if we have a p in the denominator of a fraction we are in Qp.
Note: in other sections we refer to the generators of the additive group modulo n as "generators".
| 
