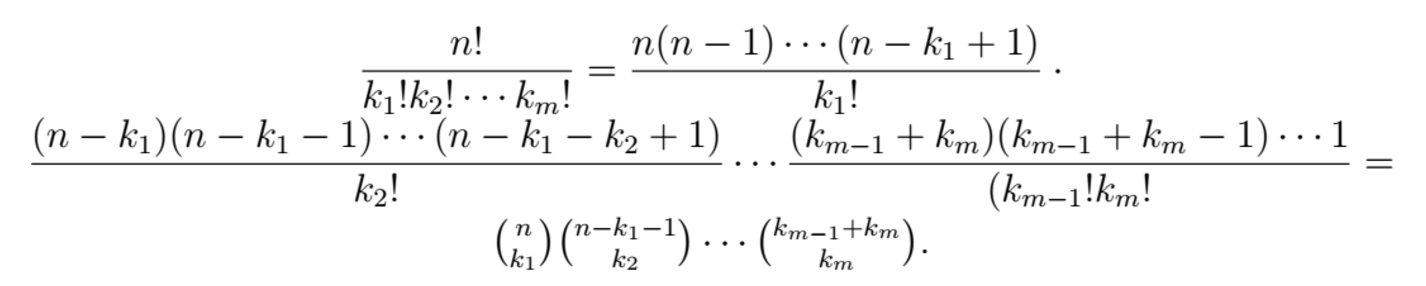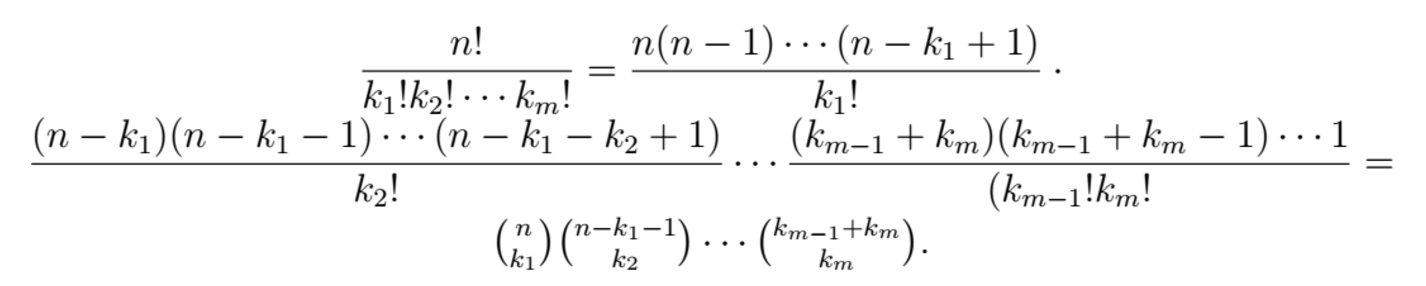LaTeX4Web 1.4 OUTPUT
In this section we generalize the Condition 1 explained in the section "An open problem" to the multinomials. The multinomial (k1, k2,...,km) is defined to be equal to (k1+k2+...+km)/(k1!k2!...km!). Therefore, given n, if we want to compute all the possible multinomial coefficients with n in the numerator we need to introduce the concept of partitions. Imagine we want n to be 5. In how many ways can we add 5? 1+1+1+1+1 (m=5) 1+1+1+2 (m=4) 1+2+2 (m=3) ; 1+1+3 (m=3) 2+3 (m=2) 1+4 (m=2) 5 (m=1)
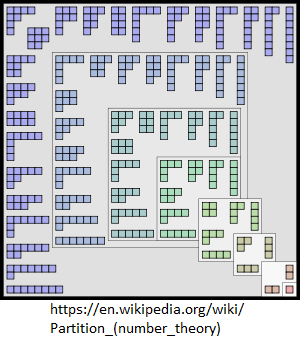
The following picture illustrates the number of partitions of n for n=1, 2, 3, 4, 5, 6, 7, 8.
Here we provide the code to compute all the partitions given n. We do so recursively.
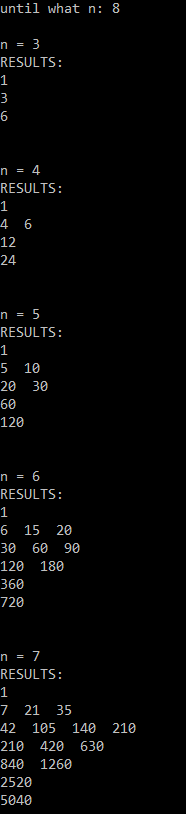
Here you can observe an example of the output of the code.
Here you can see an example of the output. The results are displayed in the same way as the code of the partitions.
LaTeX4Web 1.4 OUTPUT
We now consider the generalization of Condition 1 to the mutlinomials in the following way: Condition 2. For a given fixed integer m there exist primes p1 and p2 such that whenever k1+ \dots + km =n for 1 £ ki £ n-1, the multinomial coefficient (k1,k2,...,km) is divisible by either p1 or p2. A very natural question follows: does Condition 2 hold for all integers n? We can prove the following: Proposition. If primes p1 and p2 satisfy Condition 1 for a given n, then these two primes also satisfy Condition 2 with the same n and any m £ n. Proof: We assume that p1 and p2 satisfy Condition 1 for given n. We then take the multinomial (k1,k2,...,km) = n!/(k1!k2!...km!) with the same n and any m £ n. We see that we can decompose the multinomial into the product of m binomials:
LaTeX4Web 1.4 OUTPUT
Because by assumption C(m,k1) is divisible by either p1 or p2, the previous multinomial is also divisible by at least one of them. This decomposition can be used for any m and the first binomial coefficient can be C(n,ki), ki being any of the k in the denominator. Therefore, if Condition 1 is proven for the binomials, Condition 2 is also proven.
Finally, we provide the code for Condition 2. It returns the smallest pair of primes such that Condition 2 is satisfied for a given n.
Here you can see an example of the output of the code.