Number theory and Group theory

First we prove another case in which n satisfies the Condition 1 defined in the section "An open problem". Let q_i be the largest prime smaller than n and let p_q^a_q be any prime factor divisor of n. By checking computationally all the pairs of primes that satisfy Condition 1 for each integer, we prove the following: Theorem. If n-q_i < p_q^a_q , then n satisfies Condition 1 with p_q and q_i. For the proof of this theorem we make use of Bertrand-Chebyshev Theorem: Theorem. (Bertrand-Chebyshev) For every integer n > 3 there exists a prime p such that n/2 < p < n. Proof: For the proof of the previous theorem we distinguish between two intervals: the interval (1, n-q_i] and the interval (n-q_i, n]. Due to the symmetry of binomial coefficients, we only consider k £ n/2. By the Bertrand-Chebyshev Theorem, we know that there is at least one prime between n/2 and n, hence n/2 < q_i < n. Then, for all k, k < n/2 < q_i. The base q_i representation of n is 1 · q_i + n-q_i. Therefore, we do not need to consider the interval (n-q_i) because the last digit of the base q_i representation of any k> n-q_i is larger than the last digit of the base q_i representation of n and thus by Lucas¢ Theorem the binomial coefficient \binomnk is divisible by q_i. If also there is no multiple of p_q^a_q in the interval (1, n-q_i), then by Lucas¢ Theorem all the binomial coefficients \binomnk with 1 £ k £ n/1 are divisible by at least p_q or p_i. Moreover, the case of equality in the previous theorem cannot occur because p_q^a_q divides both p_q^a_q and n, and hence q_i would not be a prime.

Note that for the previous theorem we do not necessarily need p_q^a_q to be the largest prime power divisor of n, and therefore we have the following corollary: Corollary. Let p_j^a_j denote the largest prime power divisor of an integer n. If n - q_i < p_j^a_j , then n satisfies Condition 1 with p_j and q_i. Note that if n satisfies Condition 1 at least one of these two primes has to be a prime factor of n, because otherwise C(n,1) = n is not divisible by either of the two primes. 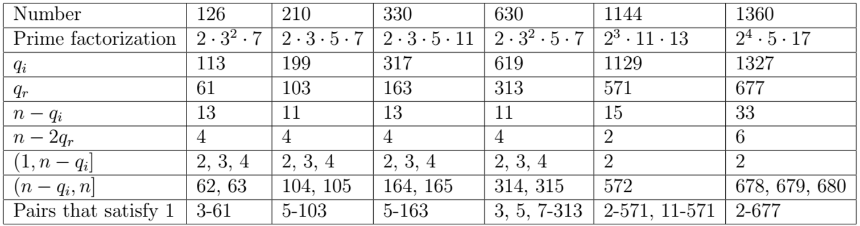Thus, the only remaining cases are those in which n - q_i > p_q^a_q and n is not a prime or a prime power. By analyzing the integers that are part of these remaining cases, we notice that n usually satisfies Condition 1 with the pair formed by a prime factor of n and the largest prime smaller than n/2. Let q_r denote the largest prime smaller than n/2. If we analyze the six numbers smaller than 2,000 such that n - q_i > p_q^a_q , we see that the inequality p_q^a_q > n-2q_r holds and q_r and p_q satisfy Condition 1. The following table shows the only six numbers until 2,000 that do not satisfy Condition 1 with q_i and p_q. However, the sequence of all such integers is infinite. The Online Encyclopedia of Integer Sequences (OEIS) has accepted our submission of this sequence with the reference A290203. Check the webpage: https://oeis.org/A290203.

Then, we can study the inequality n-q_i > p_q^a_q > n-2q_r. The fact that we are considering n-2q_r comes from the base q_r representation of n. We also computed the sequence of numbers that do not satisfy this inequality, and the OEIS has accepted our sequence with the reference A290290. Check the webpage: https://oeis.org/A290290.

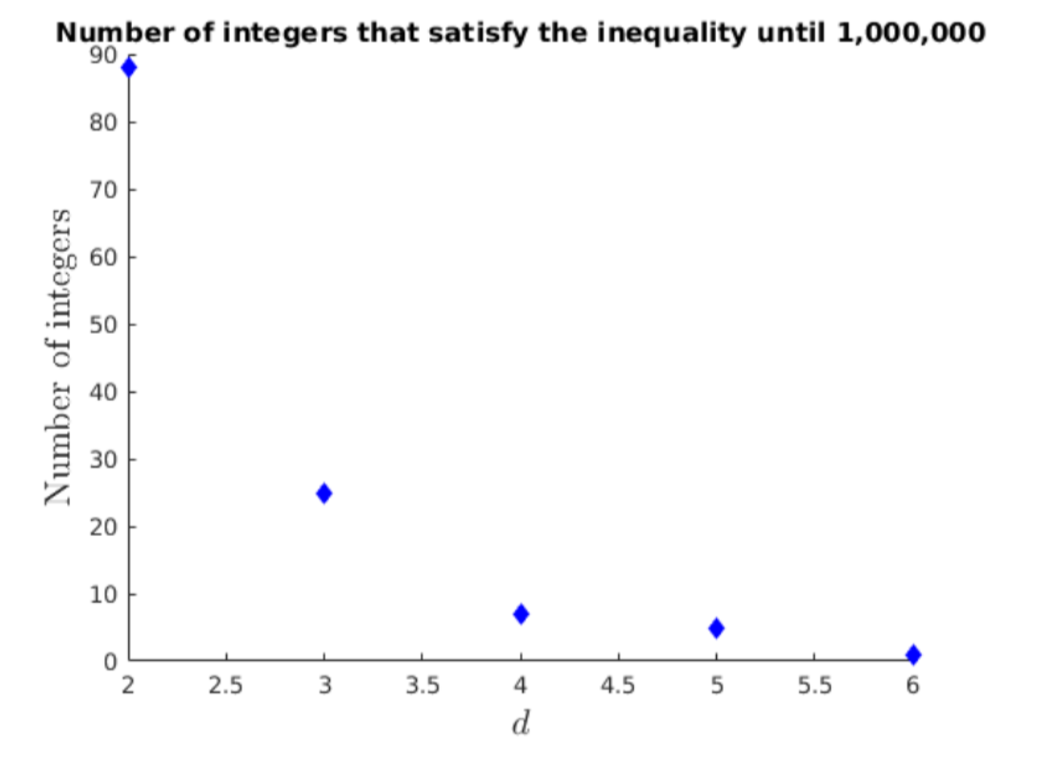
In general, for any natural integer d, we can study the function n-dq_d, where q_d refers to the closest prime to n/d. We consider the integers n that do not satisfy the inequality p_q^a_q > n-2p₂. Up to 1,000,000 there are only 88 integers that do not satisfy p_q^a_q > n-2p₂. Up to 1,000,000 there are 25 integers that do not satisfy the inequality p_q^a_q > n-3p₃. Until 1,000,000, there are 7 integers that do not satisfy the inequality p_q^a_q > n-4p₄, 5 integers that do not satisfy the inequality p_q^a_q > n-5p₅ and only 1 integer that does not satisfy the inequality p_q^a_q > n-6p₆. The following figure shows the number of integers up to 1,000,000 that do not satisfy the inequality p_q^a_q depending on d.