Using the definitions of p-adic convergence we can compute very interesting convergences regarding the factorial function.
Claim. ån=0¥
nn! = -1.
Proof: We say that a = å n!. We do not know if a is rational or not, but we can compute the following:
ån=0¥
|
((n+1)! - n!) = 1! -0! + 2! - 1! + 3! -2! + ... = -1.
Because of the alternating sign, when we go to infinity all the terms will cancel except for -0!, which is equal to -1. Then
(n+1)! - n! = n!(n+1-1) = nn!
å nn! = å nn! = -1.
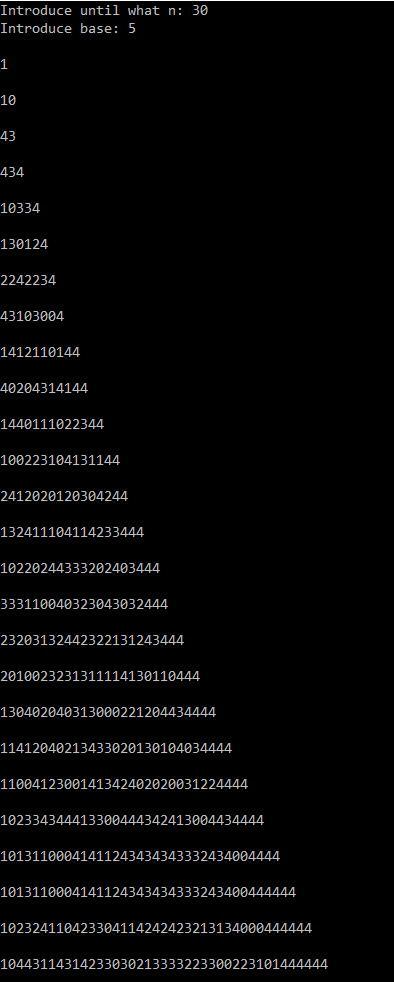
The following output of our C++ code illustrates the meaning of p-adic convergence to -1 in Z5. Note that the digit p-1, in this case 4 because -1 º 4 modulo 5 keeps repeating in the end more times as n increases.
LaTeX4Web 1.4 OUTPUT
Then we can compute å n2
|
n! using the following trick:
ån=0 (n+2)(n+1)n! = ån=0 (n+2)! = ån=2 n! = a - 1.
However, we also have that
ån=0 (n+2)(n+1)n! = ån=0 (n2
|
+ 3n + 2)n! = ån=0 n2
|
n! + 3 ån=0 nn! + 2 ån=0 n!.
Then substitutin:
ån=0 n2
|
n! + 3 ån=0 nn! + 2 ån=0 n! = ån=0 n2
|
n! -3 + 2(a +1).
Finally equating:
a -1 = ån=0¥
|
n2
|
n! -1 + 2a
ån=0 n2
|
n! = -a.
This is a recursive process and by obtaining all the values of te convergence of å_n=0 nk-1
|
n! we can obtain the value of å_n=0 nk
|
n!. We also note the following:
Claim. If å_n=0¥
|
n! is rational, then any å_n=0¥
|
nk
|
n! is also rational.
Proof: As it is seen from the recursion, it is clear that å_n=0¥
|
nk
|
n! = a a + b, where the values of a and b depend on k. Therefore, if a is rational, then so is a a + b.
Following the recursivity, we can compute the first values of å_n=0 nk
|
n!:
ån=0 n3
|
n! = a + 2
ån=0 n4
|
n! = 2 a -3
ån=0 nk
|
n! = -9 a - 4.
It is interesting to observe that if the coefficient of a is 0, then å_n=0 nk
|
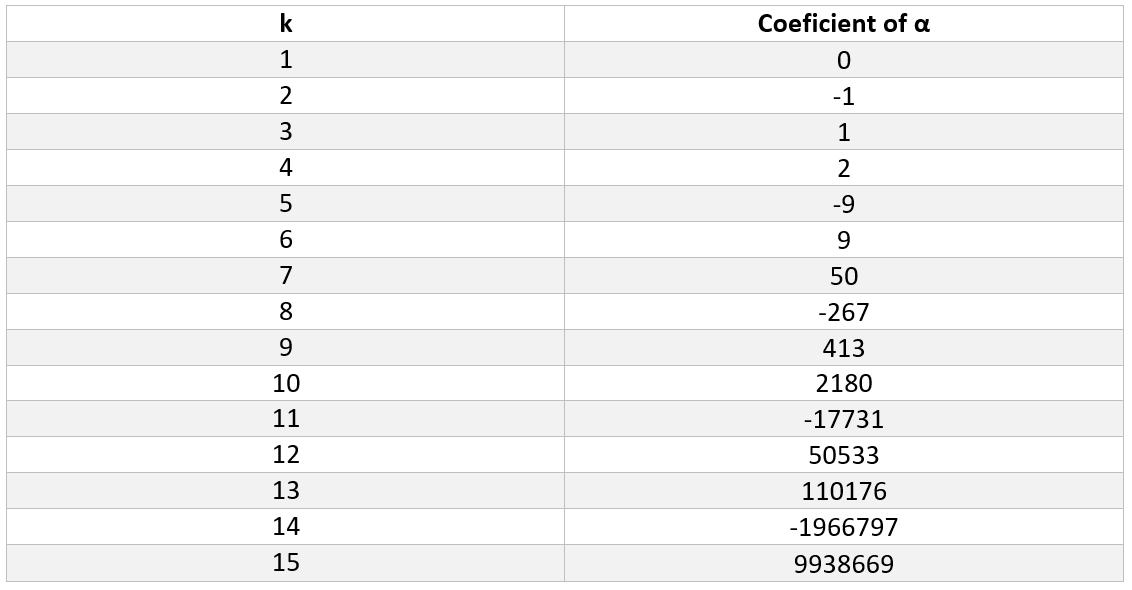
n! converges to an integer number. We have computed using C++ the coefficients of a until very large numbers, and we have encountered that it only seems to be 0 for k=1. Table 3 shows the values of the coefficient of a until k=15. We observe that the value of the coefficient of a bounces between positive and negative values, but the absolute value seems to keep increasing. This provides evidence to conjecture
the following:
Conjecture 1. The series ån=0 nk
|
n! converge to an integer number only when k=1.
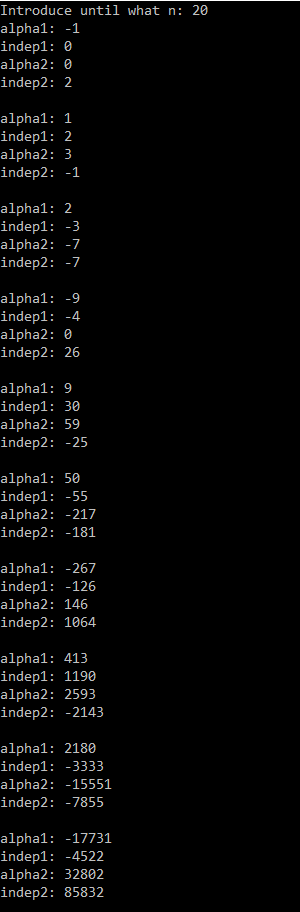
Here we provide the C++ code needed to compute the coefficients of alpha. It follows the recursive method described in this page.
Here you can see an example of the output of the code. The alphas presented in the previous table are the ones corresponding to "alpha1",
LaTeX4Web 1.4 OUTPUT
We can also generatlize these series and study the convergence of ån=1 nk
|
(n+m)!. Using a similar recursive method, we wrote a C++ that computed the coefficient of alpha of these series for each value of k and m. We found the following:
Conjecture. The series ån=1 nk
|
(n+m)! only converge to an integer for k=1, m=0,k=2, m=1 and k=5, m=1.
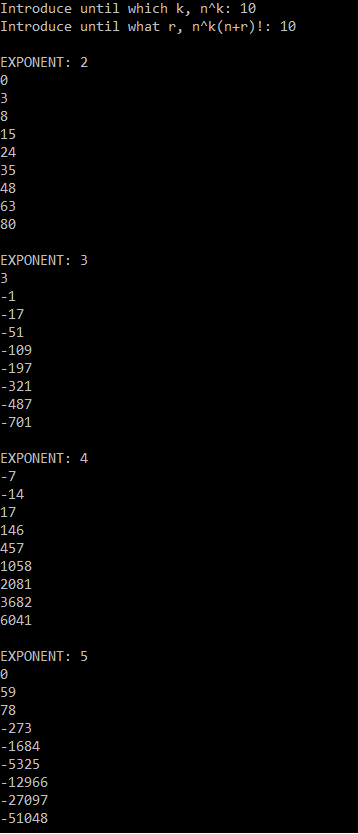
Here we provide the C++ code for computing the coefficients of alpha in the general case:
Here you can see an example of the output of the code:
If you keep running the program you will see that a zero only appears for when the exponent is equal to 2 or 5. This is what the conjecture is based on.
|