LaTeX4Web 1.4 OUTPUT
Similarly to Newton
¢s Method, in p-adic analysis we find Hensel
¢s Lemma, which allows to find the p-adic expansion of any given polynomial. Let f(x) be a polynomial function and we search its roots in the p-adic ring. First we need to define p. Then we find x
1 such that f(x
1)
º 0 mod p. Then we look for x
2. We know that it is of the form
x2 = x1 + pt and we need to determine t. We want that x
2 º x
1 modulo p. By the Taylor expansion we know that
f(x2) = f(x1 + pt) = f(x1) + ptf¢(x1) +... We do not need to write all the expansion because
f(x1) + ptf¢(x1) mod p2
. Since we know that f(x1) º 0 mod p we can divide the previous expression by p: f(x1)/p + tf¢(x1) º 0 mod p. We can find t from this expression and then we can find x2 since it was defined as x1 + pt. This steps can be done recursively similar to Newton¢s Method. In general, we use these two expressions: f(xn-1)/pn-1
|
+ tf¢(xn-1) º 0 mod p xn = xn-1 + tpn-1
|
mod pn
|
. Also similar to Newton¢s Method, the necessary condition for Hensel¢s Lemma to work is that f¢(x) ¹ 0 mod p. Also, the coefficients of the polynomials need to be reduced modulo m. We can take as an example the equation x2
|
= 5. We know that x1 equals 4 and then x2 = x1 + pt = 4 + 11t mod p2
|
. Then we find t by using the previous recursive expressions 11/11 + 8t º 0 mod p. We see that t equals 4. Then we know that x2 = 4 + 11t = 4 + 11 · 4 = 48. Using this we obtain the different ai which are 4, 4, 10, 4, 0...
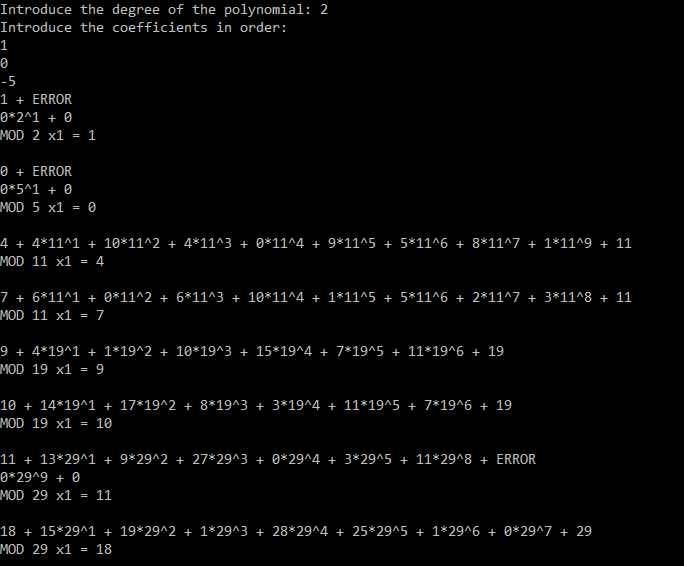
We also provide the code for Hensel's Lemma. The program will return "ERROR" if the derivative becomes zero. In the code it is possible to change until what prime should the program find expansions.
LaTeX4Web 1.4 OUTPUT
Here you can see an example of the code for the polynomial x2
|
-5.
|